AcWing 1021. 货币系统 原题链接
给你一个n种面值的货币系统,求组成面值为m的货币有多少种方案。
输入格式
第一行,包含两个整数n和m。
接下来n行,每行包含一个整数,表示一种货币的面值。
输出格式
共一行,包含一个整数,表示方案数。
数据范围
n≤15,m≤3000n≤15,m≤3000
输入样例:
3 10
1
2
5
输出样例:
10
题目思路

public static void main(String[] args) {
int n = in.nextInt();
int m = in.nextInt();
long[] dp = new long[m + 1];
int[] arr = new int[n + 1];
for (int i = 1; i <= n; i++) arr[i] = in.nextInt();
dp[0] = 1L;
for (int i = 1; i < n + 1; i++) {
for (int j = arr[i]; j <= m; j++) {
dp[j] += dp[j - arr[i]];
}
}
out.println(dp[m]);
out.flush();
out.close();
}
AcWing 532. 货币系统 原题链接
在网友的国度中共有 nn 种不同面额的货币,第 ii 种货币的面额为 a[i]a[i],你可以假设每一种货币都有无穷多张。
为了方便,我们把货币种数为 nn、面额数组为 a[1..n]a[1..n] 的货币系统记作 (n,a)(n,a)。
在一个完善的货币系统中,每一个非负整数的金额 xx 都应该可以被表示出,即对每一个非负整数 xx,都存在 nn 个非负整数 t[i]t[i] 满足 a[i]×t[i]a[i]×t[i] 的和为 xx。
然而,在网友的国度中,货币系统可能是不完善的,即可能存在金额 xx 不能被该货币系统表示出。
例如在货币系统 n=3, a=[2,5,9]n=3, a=[2,5,9] 中,金额 1,31,3 就无法被表示出来。
两个货币系统 (n,a)(n,a) 和 (m,b)(m,b) 是等价的,当且仅当对于任意非负整数 xx,它要么均可以被两个货币系统表出,要么不能被其中任何一个表出。
现在网友们打算简化一下货币系统。
他们希望找到一个货币系统 (m,b)(m,b),满足 (m,b)(m,b) 与原来的货币系统 (n,a)(n,a) 等价,且 mm 尽可能的小。
他们希望你来协助完成这个艰巨的任务:找到最小的 mm。
输入格式
输入文件的第一行包含一个整数 TT,表示数据的组数。
接下来按照如下格式分别给出 TT 组数据。
每组数据的第一行包含一个正整数 nn。
接下来一行包含 nn 个由空格隔开的正整数 a[i]a[i]。
输出格式
输出文件共有 TT 行,对于每组数据,输出一行一个正整数,表示所有与 (n,a)(n,a) 等价的货币系统 (m,b)(m,b) 中,最小的 mm。
数据范围
1≤n≤1001≤n≤100, 1≤a[i]≤250001≤a[i]≤25000, 1≤T≤201≤T≤20
输入样例:
2
4
3 19 10 6
5
11 29 13 19 17
输出样例:
2
5
题目思路

public static void main(String[] args) {
int t = in.nextInt();
while (t-- > 0) {
int n = in.nextInt();
int res = 0;
int[] arr = new int[n + 1];
for (int i = 1; i < n + 1; i++) arr[i] = in.nextInt();
Arrays.sort(arr, 1, n + 1);
//最大值就是背包容量
int[] dp = new int[arr[n] + 1];
dp[0] = 1;
for (int i = 1; i < n + 1; i++) {
//判断[1,i-1]有没有能够组成arr[i]的
if (dp[arr[i]] == 0) res++;
//利用arr[i]更新后面的方案数
for (int j = arr[i]; j <= arr[n]; j++) {
dp[j] += dp[j - arr[i]];
}
}
out.println(res);
}
out.flush();
out.close();
}
AcWing 7. 混合背包问题 原题链接
有 NN 种物品和一个容量是 VV 的背包。
物品一共有三类:
- 第一类物品只能用1次(01背包);
- 第二类物品可以用无限次(完全背包);
- 第三类物品最多只能用 sisi 次(多重背包);
每种体积是 vivi,价值是 wiwi。
求解将哪些物品装入背包,可使物品体积总和不超过背包容量,且价值总和最大。 输出最大价值。
输入格式
第一行两个整数,N,VN,V,用空格隔开,分别表示物品种数和背包容积。
接下来有 NN 行,每行三个整数 vi,wi,sivi,wi,si,用空格隔开,分别表示第 ii 种物品的体积、价值和数量。
- si=−1si=−1 表示第 ii 种物品只能用1次;
- si=0si=0 表示第 ii 种物品可以用无限次;
- si>0si>0 表示第 ii 种物品可以使用 sisi 次;
输出格式
输出一个整数,表示最大价值。
数据范围
0<N,V≤10000<N,V≤1000 0<vi,wi≤10000<vi,wi≤1000 −1≤si≤1000−1≤si≤1000
输入样例
4 5
1 2 -1
2 4 1
3 4 0
4 5 2
输出样例:
8
private static class Goods {
private int volume;
private int value;
private int type;
public Goods(int volume, int value, int type) {
this.volume = volume;
this.value = value;
this.type = type;
}
}
public static void main(String[] args) {
int n = in.nextInt();
int m = in.nextInt();
Goods[] goods = new Goods[n + 1];
int[] dp = new int[m + 1];
for (int i = 1; i < n + 1; i++) {
goods[i] = new Goods(in.nextInt(), in.nextInt(), in.nextInt());
}
for (int i = 1; i < n + 1; i++) {
int s = goods[i].type;
if (s == 0) {
for (int j = goods[i].volume; j <= m; j++) {
dp[j] = Math.max(dp[j], dp[j - goods[i].volume] + goods[i].value);
}
} else {
//01背包看成特殊的多重背包
if (s == -1) s = 1;
//二进制打包
for (int j = 1; s >= j; s -= j, j <<= 1) {
//01背包过程
for (int k = m; k >= j * goods[i].volume; k--) {
dp[k] = Math.max(dp[k], dp[k - j * goods[i].volume] + j * goods[i].value);
}
}
//打包剩下的
if (s > 0) {
for (int k = m; k >= s * goods[i].volume; k--) {
dp[k] = Math.max(dp[k], dp[k - s * goods[i].volume] + s * goods[i].value);
}
}
}
}
out.println(dp[m]);
out.flush();
out.close();
}
AcWing 10. 有依赖的背包问题 原题链接
有 NN 个物品和一个容量是 VV 的背包。
物品之间具有依赖关系,且依赖关系组成一棵树的形状。如果选择一个物品,则必须选择它的父节点。
如下图所示:
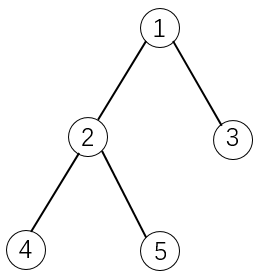
如果选择物品5,则必须选择物品1和2。这是因为2是5的父节点,1是2的父节点。
每件物品的编号是 ii,体积是 vivi,价值是 wiwi,依赖的父节点编号是 pipi。物品的下标范围是 1…N1…N。
求解将哪些物品装入背包,可使物品总体积不超过背包容量,且总价值最大。
输出最大价值。
输入格式
第一行有两个整数 N,VN,V,用空格隔开,分别表示物品个数和背包容量。
接下来有 NN 行数据,每行数据表示一个物品。 第 ii 行有三个整数 vi,wi,pivi,wi,pi,用空格隔开,分别表示物品的体积、价值和依赖的物品编号。 如果 pi=−1pi=−1,表示根节点。 数据保证所有物品构成一棵树。
输出格式
输出一个整数,表示最大价值。
数据范围
1≤N,V≤1001≤N,V≤100 1≤vi,wi≤1001≤vi,wi≤100
父节点编号范围:
- 内部结点:1≤pi≤N1≤pi≤N;
- 根节点 pi=−1pi=−1;
输入样例
5 7
2 3 -1
2 2 1
3 5 1
4 7 2
3 6 2
输出样例:
11
题目思路

static List<List<Integer>> graph = new ArrayList<>();
static Goods[] goods;
static int[][] dp;
static int n;
static int m;
private static class Goods{
private int volume;
private int value;
public Goods(int volume, int value) {
this.volume = volume;
this.value = value;
}
}
private static void add(int a, int b) {
graph.get(b).add(a);
}
private static void dfs(int u) {
List<Integer> list = graph.get(u);
for (int x : list) {
dfs(x);
//根节点是必选的,说剩下体积就是m-goods[u].volume
//分组背包过程
for (int j = m - goods[u].volume; j >= 0; j--) {
//枚举子树所占[0,j]体积的方案
for (int k = 0; k <= j; k++) {
dp[u][j] = Math.max(dp[u][j], dp[u][j - k] + dp[x][k]);
}
}
}
//每个方案需要加上本身选择root的价值
for (int i = m; i >= goods[u].volume; i--) {
dp[u][i] = dp[u][i - goods[u].volume] + goods[u].value;
}
//对于背包体积装不下root的情况,设置为0
for (int i = 0; i < goods[u].volume; i++) dp[u][i] = 0;
}
public static void main(String[] args) {
n = in.nextInt();
m = in.nextInt();
goods = new Goods[n + 1];
dp = new int[n + 1][m + 1];
for (int i = 0; i < n + 1; i++) graph.add(new ArrayList<>());
int root = -1;
for (int i = 1; i < n + 1; i++) {
int volume = in.nextInt();
int value = in.nextInt();
int dependence = in.nextInt();
goods[i] = new Goods(volume, value);
if (dependence == -1) {
root = i;
continue;
}
add(i, dependence);
}
dfs(root);
out.println(dp[root][m]);
out.flush();
out.close();
}
AcWing 11. 背包问题求方案数 原题链接
有 NN 件物品和一个容量是 VV 的背包。每件物品只能使用一次。
第 ii 件物品的体积是 vivi,价值是 wiwi。
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。
输出 最优选法的方案数。注意答案可能很大,请输出答案模 109+7109+7 的结果。
输入格式
第一行两个整数,N,VN,V,用空格隔开,分别表示物品数量和背包容积。
接下来有 NN 行,每行两个整数 vi,wivi,wi,用空格隔开,分别表示第 ii 件物品的体积和价值。
输出格式
输出一个整数,表示 方案数 模 109+7109+7 的结果。
数据范围
0<N,V≤10000<N,V≤1000 0<vi,wi≤10000<vi,wi≤1000
输入样例
4 5
1 2
2 4
3 4
4 6
输出样例:
2
题目思路

朴素算法:
private static void function1() {
int n = in.nextInt();
int m = in.nextInt();
int mod = (int)(1e9 + 7);
Goods[] goods = new Goods[n + 1];
for (int i = 1; i < n + 1; i++) goods[i] = new Goods(in.nextInt(), in.nextInt());
int[][] dp = new int[n + 1][m + 1];
int[][] g = new int[n + 1][m + 1];
for (int i = 0; i < n + 1; i++) Arrays.fill(dp[i], Integer.MIN_VALUE);
//从前i个选,体积为0最大值都为0
for (int i = 0; i < n + 1; i++) dp[i][0] = 0;
//从前i个选,体积为0,最优选法都是不选,即为一种
for (int j = 0; j < m + 1; j++) g[0][j] = 1;
for (int i = 1; i < n + 1; i++) {
for (int j = 0; j < m + 1; j++) {
int max = dp[i - 1][j];
if (j >= goods[i].volume) {
max = Math.max(max, dp[i - 1][j - goods[i].volume] + goods[i].value);
}
if (max == dp[i - 1][j]) g[i][j] = (g[i][j] + g[i - 1][j]) % mod;
if (j >= goods[i].volume && max == dp[i - 1][j - goods[i].volume] + goods[i].value) g[i][j] = (g[i][j] + g[i - 1][j - goods[i].volume]) % mod;
dp[i][j] = max;
}
}
int max = 0;
for (int j = 0; j < m + 1; j++) max = Math.max(max, dp[n][j]);
int res = 0;
for (int j = 0; j < m + 1; j++) {
if (dp[n][j] == max) res = (res + g[n][j]) % mod;
}
out.println(res);
out.flush();
out.close();
}
空间优化写法:
private static void function2() {
int n = in.nextInt();
int m = in.nextInt();
int mod = (int)(1e9 + 7);
Goods[] goods = new Goods[n + 1];
for (int i = 1; i < n + 1; i++) goods[i] = new Goods(in.nextInt(), in.nextInt());
int[] dp = new int[m + 1]; int[] g = new int[m + 1];
Arrays.fill(dp, Integer.MIN_VALUE);
dp[0] = 0; g[0] = 1;
for (int i = 1; i < n + 1; i++) {
for (int j = m; j >= goods[i].volume; j--) {
int max = Math.max(dp[j], dp[j - goods[i].volume] + goods[i].value);
if (max != dp[j]) g[j] = 0;
if (max == dp[j - goods[i].volume] + goods[i].value) g[j] = (g[j] + g[j - goods[i].volume]) % mod;
dp[j] = max;
}
}
int max = 0;
int res = 0;
for (int j = 0; j < m + 1; j++) max = Math.max(max, dp[j]);
for (int j = 0; j < m + 1; j++) {
if (dp[j] == max) {
res = (res + g[j]) % mod;
}
}
out.println(res);
out.flush();
out.close();
}
AcWing 734. 能量石 原题链接
岩石怪物杜达生活在魔法森林中,他在午餐时收集了N块能量石准备开吃。
由于他的嘴很小,所以一次只能吃一块能量石。
能量石很硬,吃完需要花不少时间。
吃完第 i 块能量石需要花费的时间为SiSi秒。
杜达靠吃能量石来获取能量。
不同的能量石包含的能量可能不同。
此外,能量石会随着时间流逝逐渐失去能量。
第 i 块能量石最初包含EiEi单位的能量,并且每秒将失去LiLi单位的能量。
当杜达开始吃一块能量石时,他就会立即获得该能量石所含的全部能量(无论实际吃完该石头需要多少时间)。
能量石中包含的能量最多降低至0。
请问杜达通过吃能量石可以获得的最大能量是多少?
输入格式
第一行包含整数T,表示共有T组测试数据。
每组数据第一行包含整数N,表示能量石的数量。
接下来N行,每行包含三个整数Si,Ei,LiSi,Ei,Li。
输出格式
每组数据输出一个结果,每个结果占一行。
结果表示为“Case #x: y”,其中x是组别编号(从1开始),y是可以获得的最大能量值。
数据范围
1≤T≤101≤T≤10, 1≤N≤1001≤N≤100, 1≤Si≤1001≤Si≤100, 1≤Ei≤1051≤Ei≤105, 0≤Li≤1050≤Li≤105
输入样例:
3
4
20 10 1
5 30 5
100 30 1
5 80 60
3
10 4 1000
10 3 1000
10 8 1000
2
12 300 50
5 200 0
输出样例:
Case #1: 105
Case #2: 8
Case #3: 500
样例解释
在样例#1中,有N = 4个宝石。杜达可以选择的一个吃石头顺序是:
- 吃第四块石头。这需要5秒,并给他80单位的能量。
- 吃第二块石头。这需要5秒,并给他5单位的能量(第二块石头开始时具有30单位能量,5秒后失去了25单位的能量)。
- 吃第三块石头。这需要100秒,并给他20单位的能量(第三块石头开始时具有30单位能量,10秒后失去了10单位的能量)。
- 吃第一块石头。这需要20秒,并给他0单位的能量(第一块石头以10单位能量开始,110秒后已经失去了所有的能量)。
他一共获得了105单位的能量,这是能获得的最大值,所以答案是105。
在样本案例#2中,有N = 3个宝石。
无论杜达选择吃哪块石头,剩下的两个石头的能量都会耗光。
所以他应该吃第三块石头,给他提供8单位的能量。
在样本案例#3中,有N = 2个宝石。杜达可以:
- 吃第一块石头。这需要12秒,并给他300单位的能量。
- 吃第二块石头。这需要5秒,并给他200单位的能量(第二块石头随着时间的推移不会失去任何能量!)。
所以答案是500。
题目思路

private static class Stone implements Comparable<Stone>{
private int time;
private int energy;
private int decrease;
public Stone(int time, int energy, int decrease) {
this.time = time;
this.energy = energy;
this.decrease = decrease;
}
@Override
public int compareTo(Stone o) {
return Integer.compare(this.time * o.decrease, this.decrease * o.time);
}
}
public static void main(String[] args) {
int t = in.nextInt();
for (int T = 1; T <= t; T++) {
int n = in.nextInt();
int m = 0;
Stone[] stones = new Stone[n + 1];
for (int i = 1; i < n + 1; i++) {
int s = in.nextInt();
int e = in.nextInt();
int l = in.nextInt();
stones[i] = new Stone(s, e, l);
m += s;
}
int[] dp = new int[m + 1];
Arrays.fill(dp, Integer.MIN_VALUE);
dp[0] = 0;
Arrays.sort(stones, 1, n + 1);
for (int i = 1; i < n + 1; i++) {
for (int j = m; j >= stones[i].time; j--) {
//注意能量是会随着时间变短的,实际退减时间为(j-stones[i].time)而不是j
//因为石头在吃到的瞬间就不会退减了,stones[i].time只是消化时间
//能量不能递减到小于0
int decreaseTime = j - stones[i].time;
dp[j] = Math.max(dp[j], dp[j - stones[i].time] + Math.max(0, stones[i].energy - decreaseTime * stones[i].decrease));
}
}
int res = 0;
for (int j = 0; j <= m; j++) res = Math.max(res, dp[j]);
out.println("Case #" + T +": " + res);
}
out.flush();
out.close();
}
