AcWing 12. 背包问题求具体方案 原题链接
有 NN 件物品和一个容量是 VV 的背包。每件物品只能使用一次。
第 ii 件物品的体积是 vivi,价值是 wiwi。
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。
输出 字典序最小的方案。这里的字典序是指:所选物品的编号所构成的序列。物品的编号范围是 1…N1…N。
输入格式
第一行两个整数,N,VN,V,用空格隔开,分别表示物品数量和背包容积。
接下来有 NN 行,每行两个整数 vi,wivi,wi,用空格隔开,分别表示第 ii 件物品的体积和价值。
输出格式
输出一行,包含若干个用空格隔开的整数,表示最优解中所选物品的编号序列,且该编号序列的字典序最小。
物品编号范围是 1…N1…N。
数据范围
0<N,V≤10000<N,V≤1000 0<vi,wi≤10000<vi,wi≤1000
输入样例
4 5
1 2
2 4
3 4
4 6
输出样例:
1 4
题目思路
可以记录每一次的具体选择
由于这个题目需要输出字典序最小的选择,从前往后遍历时每次选择有三种情况:
- 必须选择
- 必须不选择
- 可选可不选时:必须选择

朴素写法:
private static void function1() {
int n = in.nextInt();
int m = in.nextInt();
Goods[] goods = new Goods[n + 2];
int[][] dp = new int[n + 2][m + 1];
int[][] path = new int[n + 2][m + 1];
for (int i = 1; i < n + 1; i++) goods[i] = new Goods(in.nextInt(), in.nextInt());
for (int i = n; i >= 1; i--) {
for (int j = 0; j <= m; j++) {
dp[i][j] = dp[i + 1][j];
if (j >= goods[i].volume && dp[i][j] <= dp[i + 1][j - goods[i].volume] + goods[i].value) {
dp[i][j] = dp[i + 1][j - goods[i].volume] + goods[i].value;
path[i][j] = 1;
}
}
}
int c = m;
for (int i = 1; i < n + 1; i++) {
if (path[i][c] == 1) {
out.print(i + " ");
c -= goods[i].volume;
}
}
out.flush();
out.close();
}
空间优化写法:
private static void function2() {
int n = in.nextInt();
int m = in.nextInt();
Goods[] goods = new Goods[n + 2];
int[] dp = new int[m + 1];
int[][] path = new int[n + 2][m + 1];
for (int i = 1; i < n + 1; i++) goods[i] = new Goods(in.nextInt(), in.nextInt());
for (int i = n; i >= 1; i--) {
for (int j = m; j >= 0; j--) {
if (j >= goods[i].volume && dp[j] <= dp[j - goods[i].volume] + goods[i].value) {
dp[j] = dp[j - goods[i].volume] + goods[i].value;
path[i][j] = 1;
}
}
}
int c = m;
for (int i = 1; i < n + 1; i++) {
if (path[i][c] == 1) {
out.print(i + " ");
c -= goods[i].volume;
}
}
out.flush();
out.close();
}
AcWing 1013. 机器分配 原题链接
总公司拥有M台 相同 的高效设备,准备分给下属的N个分公司。
各分公司若获得这些设备,可以为国家提供一定的盈利。盈利与分配的设备数量有关。
问:如何分配这M台设备才能使国家得到的盈利最大?
求出最大盈利值。
分配原则:每个公司有权获得任意数目的设备,但总台数不超过设备数M。
输入格式
第一行有两个数,第一个数是分公司数N,第二个数是设备台数M;
接下来是一个N*M的矩阵,矩阵中的第 i 行第 j 列的整数表示第 i 个公司分配 j 台机器时的盈利。
输出格式
第一行输出最大盈利值;
接下N行,每行有2个数,即分公司编号和该分公司获得设备台数。
答案不唯一,输入任意合法方案即可。
数据范围
1≤N≤101≤N≤10, 1≤M≤151≤M≤15
输入样例:
3 3
30 40 50
20 30 50
20 25 30
输出样例:
70
1 1
2 1
3 1
题目思路
按公司分组,总体积就是机器总数,给公司分配1,2,3…j台机器看成同一分组中不同的物品,公司获利看成是物品的价值
整个物品就能转化成分组背包问题
朴素写法:
private static void function1() {
int n = in.nextInt();
int m = in.nextInt();
Goods[] goods = new Goods[n + 2];
int[][] dp = new int[n + 2][m + 1];
int[][] path = new int[n + 2][m + 1];
for (int i = 1; i < n + 1; i++) goods[i] = new Goods(in.nextInt(), in.nextInt());
for (int i = n; i >= 1; i--) {
for (int j = 0; j <= m; j++) {
dp[i][j] = dp[i + 1][j];
if (j >= goods[i].volume && dp[i][j] <= dp[i + 1][j - goods[i].volume] + goods[i].value) {
dp[i][j] = dp[i + 1][j - goods[i].volume] + goods[i].value;
path[i][j] = 1;
}
}
}
int c = m;
for (int i = 1; i < n + 1; i++) {
if (path[i][c] == 1) {
out.print(i + " ");
c -= goods[i].volume;
}
}
out.flush();
out.close();
}
空间优化写法:
private static void function2() {
int n = in.nextInt();
int m = in.nextInt();
Goods[] goods = new Goods[n + 2];
int[] dp = new int[m + 1];
int[][] path = new int[n + 2][m + 1];
for (int i = 1; i < n + 1; i++) goods[i] = new Goods(in.nextInt(), in.nextInt());
for (int i = n; i >= 1; i--) {
for (int j = m; j >= 0; j--) {
if (j >= goods[i].volume && dp[j] <= dp[j - goods[i].volume] + goods[i].value) {
dp[j] = dp[j - goods[i].volume] + goods[i].value;
path[i][j] = 1;
}
}
}
int c = m;
for (int i = 1; i < n + 1; i++) {
if (path[i][c] == 1) {
out.print(i + " ");
c -= goods[i].volume;
}
}
out.flush();
out.close();
}
AcWing 426. 开心的金明 原题链接
金明今天很开心,家里购置的新房就要领钥匙了,新房里有一间他自己专用的很宽敞的房间。
更让他高兴的是,妈妈昨天对他说:“你的房间需要购买哪些物品,怎么布置,你说了算,只要不超过 NN 元钱就行”。
今天一早金明就开始做预算,但是他想买的东西太多了,肯定会超过妈妈限定的 NN 元。
于是,他把每件物品规定了一个重要度,分为 55 等:用整数 1∼51∼5 表示,第 55 等最重要。
他还从因特网上查到了每件物品的价格(都是整数元)。
他希望在不超过 NN 元(可以等于 NN 元)的前提下,使每件物品的价格与重要度的乘积的总和最大。
设第 jj 件物品的价格为 v[j]v[j],重要度为 w[j]w[j],共选中了 kk 件物品,编号依次为 j1,j2,…,jkj1,j2,…,jk,则所求的总和为:
v[j1]×w[j1]+v[j2]×w[j2]+…+v[jk]×w[jk]v[j1]×w[j1]+v[j2]×w[j2]+…+v[jk]×w[jk]
请你帮助金明设计一个满足要求的购物单。
输入格式
输入文件的第 11 行,为两个正整数 NN 和 mm,用一个空格隔开。(其中 NN 表示总钱数,mm 为希望购买物品的个数)
从第 22 行到第 m+1m+1 行,第 jj 行给出了编号为 j−1j−1 的物品的基本数据,每行有 22 个非负整数 vv 和 pp。(其中 vv 表示该物品的价格,pp 表示该物品的重要度)
输出格式
输出文件只有一个正整数,为不超过总钱数的物品的价格与重要度乘积的总和的最大值(数据保证结果不超过 108108)。
数据范围
1≤N<300001≤N<30000, 1≤m<251≤m<25, 0≤v≤100000≤v≤10000, 1≤p≤51≤p≤5
输入样例:
1000 5
800 2
400 5
300 5
400 3
200 2
输出样例:
3900
public static void main(String[] args) {
int m = in.nextInt();
int n = in.nextInt();
int[] dp = new int[m + 1];
Goods[] goods = new Goods[n + 1];
for (int i = 1; i < n + 1; i++) {
int price = in.nextInt();
goods[i] = new Goods(price, in.nextInt() * price);
}
for (int i = 1; i < n + 1; i++) {
for (int j = m; j >= goods[i].price; j--) {
dp[j] = Math.max(dp[j], dp[j - goods[i].price] + goods[i].value);
}
}
out.println(dp[m]);
out.flush();
out.close();
}
AcWing 487. 金明的预算方案 原题链接
金明今天很开心,家里购置的新房就要领钥匙了,新房里有一间金明自己专用的很宽敞的房间。
更让他高兴的是,妈妈昨天对他说:“你的房间需要购买哪些物品,怎么布置,你说了算,只要不超过N元钱就行”。
今天一早,金明就开始做预算了,他把想买的物品分为两类:主件与附件,附件是从属于某个主件的,下表就是一些主件与附件的例子:
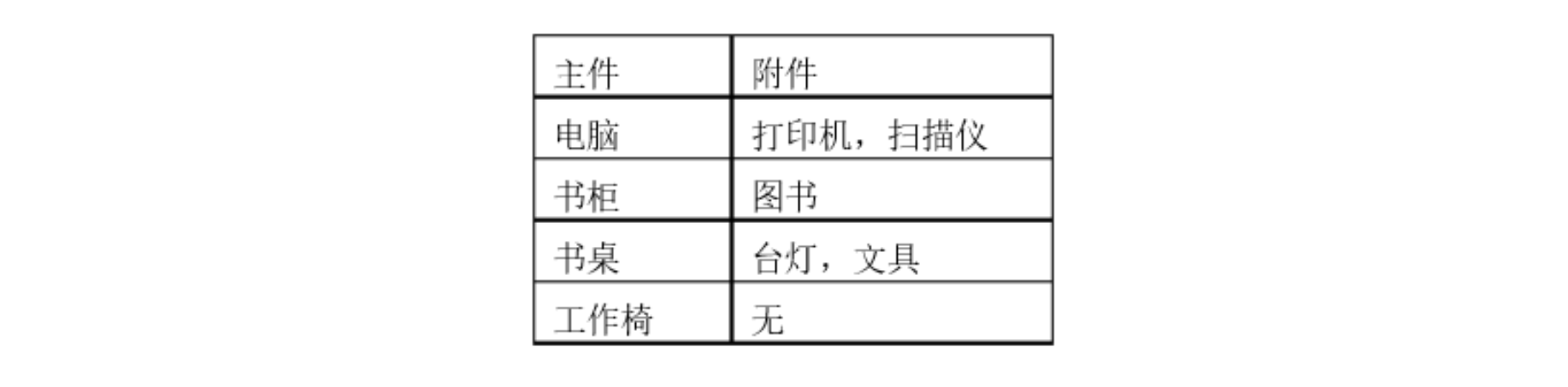
如果要买归类为附件的物品,必须先买该附件所属的主件。
每个主件可以有0个、1个或2个附件。
附件不再有从属于自己的附件。
金明想买的东西很多,肯定会超过妈妈限定的N元。
于是,他把每件物品规定了一个重要度,分为5等:用整数1~5表示,第5等最重要。
他还从因特网上查到了每件物品的价格(都是10元的整数倍)。
他希望在不超过N元(可以等于N元)的前提下,使每件物品的价格与重要度的乘积的总和最大。
设第j件物品的价格为v[j],重要度为w[j],共选中了k件物品,编号依次为j1,j2,…,jkj1,j2,…,jk,则所求的总和为:
v[j1]∗w[j1]+v[j2]∗w[j2]+…+v[jk]∗w[jk]v[j1]∗w[j1]+v[j2]∗w[j2]+…+v[jk]∗w[jk](其中*为乘号)
请你帮助金明设计一个满足要求的购物单。
输入格式
输入文件的第1行,为两个正整数,用一个空格隔开:N m,其中N表示总钱数,m为希望购买物品的个数。
从第2行到第m+1行,第j行给出了编号为j-1的物品的基本数据,每行有3个非负整数v p q,其中v表示该物品的价格,p表示该物品的重要度(1~5),q表示该物品是主件还是附件。
如果q=0,表示该物品为主件,如果q>0,表示该物品为附件,q是所属主件的编号。
输出格式
输出文件只有一个正整数,为不超过总钱数的物品的价格与重要度乘积的总和的最大值(<200000)。
数据范围
N<32000,m<60,v<10000N<32000,m<60,v<10000
输入样例:
1000 5
800 2 0
400 5 1
300 5 1
400 3 0
500 2 0
输出样例:
2200
题目思路
每件物品的组件和附件的组合选择看成分组中的一种物品,问题就能转化成为分组背包问题
private static class Combination {
private int price;
private int value;
public Combination(int price, int value) {
this.price = price;
this.value = value;
}
}
public static void main(String[] args) {
int m = in.nextInt();
int n = in.nextInt();
List<Combination>[] combinations = new ArrayList[n + 1];
for (int i = 0; i < n + 1; i++) combinations[i] = new ArrayList<>();
int[] dp = new int[m + 1];
for (int i = 1; i < n + 1; i++) {
int price = in.nextInt();
int weight = in.nextInt();
int p = in.nextInt();
if (p != 0) {
List<Combination> list = new ArrayList<>(combinations[p]);
List<Combination> clist = combinations[p];
for (Combination c : list) {
clist.add(new Combination(c.price + price, c.value + price * weight));
}
}else {
combinations[i].add(new Combination(price, price * weight));
}
}
for (int i = 1; i < n + 1; i++) {
for (int j = m; j >= 0; j--) {
for (int k = 0; k < combinations[i].size(); k++) {
Combination c = combinations[i].get(k);
if (j >= c.price) {
dp[j] = Math.max(dp[j], dp[j - c.price] + c.value);
}
}
}
}
out.println(dp[m]);
out.flush();
out.close();
}
二进制枚举写法:
//二进制枚举
private static void function2() {
int m = in.nextInt();
int n = in.nextInt();
int[] dp = new int[m + 1];
Accessories[] master = new Accessories[n + 1];
List<Accessories>[] accessories = new ArrayList[n + 1];
for (int i = 0; i <= n; i++) accessories[i] = new ArrayList<>();
for (int i = 1; i < n + 1; i++) {
int p = in.nextInt();
int w = in.nextInt();
int q = in.nextInt();
if (q != 0) accessories[q].add(new Accessories(p, w * p));
else master[i] = new Accessories(p, p * w);
}
for (int i = 1; i < n + 1; i++) {
if (master[i] == null) continue;
for (int j = m; j >= 0; j--) {
for (int x = 0; x < (1 << accessories[i].size()); x++) {
int price = master[i].price;
int value = master[i].value;
for (int k = 0; k < accessories[i].size(); k++) {
if ((1 & (x >> k)) == 1) {
price += accessories[i].get(k).price;
value += accessories[i].get(k).value;
}
}
if (j >= price) dp[j] = Math.max(dp[j], dp[j - price] + value);
}
}
}
out.println(dp[m]);
out.flush();
out.close();
}
