AcWing 8. 二维费用的背包问题 原题链接
有 NN 件物品和一个容量是 VV 的背包,背包能承受的最大重量是 MM。
每件物品只能用一次。体积是 vivi,重量是 mimi,价值是 wiwi。
求解将哪些物品装入背包,可使物品总体积不超过背包容量,总重量不超过背包可承受的最大重量,且价值总和最大。 输出最大价值。
输入格式
第一行两个整数,N,V,MN,V,M,用空格隔开,分别表示物品件数、背包容积和背包可承受的最大重量。
接下来有 NN 行,每行三个整数 vi,mi,wivi,mi,wi,用空格隔开,分别表示第 ii 件物品的体积、重量和价值。
输出格式
输出一个整数,表示最大价值。
数据范围
0<N≤10000<N≤1000 0<V,M≤1000<V,M≤100 0<vi,mi≤1000<vi,mi≤100 0<wi≤10000<wi≤1000
输入样例
4 5 6
1 2 3
2 4 4
3 4 5
4 5 6
输出样例:
8
题目思路

数据结构:
private static class Goods {
private int volume;
private int weight;
private int value;
public Goods(int volume, int weight, int value) {
this.volume = volume;
this.weight = weight;
this.value = value;
}
}
朴素写法:
private static void function1() {
int n = in.nextInt();
int v = in.nextInt();
int w = in.nextInt();
int[][][] dp = new int[n + 1][v + 1][w + 1];
Goods[] goods = new Goods[n + 1];
for (int i = 1; i < n + 1; i++) goods[i] = new Goods(in.nextInt(), in.nextInt(), in.nextInt());
for (int i = 1; i < n + 1; i++) {
for (int j = 1; j < v + 1; j++) {
for (int k = 1; k < w + 1; k++) {
dp[i][j][k] = dp[i - 1][j][k];
if (j >= goods[i].volume && k >= goods[i].weight) {
dp[i][j][k] = Math.max(dp[i][j][k], dp[i - 1][j - goods[i].volume][k - goods[i].weight] + goods[i].value);
}
}
}
}
out.println(dp[n][v][w]);
out.flush();
out.close();
}
空间优化写法:
private static void function2() {
int n = in.nextInt();
int v = in.nextInt();
int w = in.nextInt();
int[][] dp = new int[v + 1][w + 1];
Goods[] goods = new Goods[n + 1];
for (int i = 1; i < n + 1; i++) goods[i] = new Goods(in.nextInt(), in.nextInt(), in.nextInt());
for (int i = 1; i <= n; i++) {
for (int j = v; j >= goods[i].volume; j--) {
for (int k = w; k >= goods[i].weight; k--) {
dp[j][k] = Math.max(dp[j][k], dp[j - goods[i].volume][k - goods[i].weight] + goods[i].value);
}
}
}
out.println(dp[v][w]);
out.flush();
out.close();
}
AcWing 1020. 潜水员 原题链接
潜水员为了潜水要使用特殊的装备。
他有一个带2种气体的气缸:一个为氧气,一个为氮气。
让潜水员下潜的深度需要各种数量的氧和氮。
潜水员有一定数量的气缸。
每个气缸都有重量和气体容量。
潜水员为了完成他的工作需要特定数量的氧和氮。
他完成工作所需气缸的总重的最低限度的是多少?
例如:潜水员有5个气缸。每行三个数字为:氧,氮的(升)量和气缸的重量:
3 36 120
10 25 129
5 50 250
1 45 130
4 20 119
如果潜水员需要5升的氧和60升的氮则总重最小为249(1,2或者4,5号气缸)。
你的任务就是计算潜水员为了完成他的工作需要的气缸的重量的最低值。
输入格式
第一行有2个整数 m,nm,n。它们表示氧,氮各自需要的量。
第二行为整数 kk 表示气缸的个数。
此后的 kk 行,每行包括ai,bi,ciai,bi,ci,3个整数。这些各自是:第 ii 个气缸里的氧和氮的容量及气缸重量。
输出格式
仅一行包含一个整数,为潜水员完成工作所需的气缸的重量总和的最低值。
数据范围
1≤m≤211≤m≤21, 1≤n≤791≤n≤79, 1≤k≤10001≤k≤1000, 1≤ai≤211≤ai≤21, 1≤bi≤791≤bi≤79, 1≤ci≤8001≤ci≤800
输入样例:
5 60
5
3 36 120
10 25 129
5 50 250
1 45 130
4 20 119
输出样例:
249
题目思路
三种问法:
- 体积最多是j:初始化全为0,V>=0
- 体积恰好是j:f(0)=0,其余INF,V>=0
- 体积至少是j:f(0)=0,其余INF

数据结构:
private static class Cylinder {
private int oxygen;
private int nitrogen;
private int weight;
public Cylinder(int oxygen, int nitrogen, int weight) {
this.oxygen = oxygen;
this.nitrogen = nitrogen;
this.weight = weight;
}
}
朴素写法:
private static void function1() {
int n = in.nextInt();
int m = in.nextInt();
int q = in.nextInt();
int[][][] dp = new int[q + 1][n + 1][m + 1];
Cylinder[] cylinders = new Cylinder[q + 1];
for (int i = 1; i <= q; i++) cylinders[i] = new Cylinder(in.nextInt(), in.nextInt(), in.nextInt());
for (int i = 0; i < q + 1; i++)
for (int j = 0; j < n + 1; j++) {
for (int k = 0; k < m + 1; k++) {
dp[i][j][k] = Integer.MAX_VALUE / 2;
}
}
for (int i = 0; i < q + 1; i++) dp[i][0][0] = 0;
for (int i = 1; i < q + 1; i++) {
for (int j = 0; j < n + 1; j++) {
for (int k = 0; k < m + 1; k++) {
dp[i][j][k] = Math.min(dp[i - 1][j][k],
dp[i - 1][Math.max(0, j - cylinders[i].oxygen)][Math.max(0, k - cylinders[i].nitrogen)] + cylinders[i].weight
);
}
}
}
out.println(dp[q][n][m]);
out.flush();
out.close();
}
空间优化写法:
private static void function2() {
int n = in.nextInt();
int m = in.nextInt();
int q = in.nextInt();
int[][] dp = new int[n + 1][m + 1];
Cylinder[] cylinders = new Cylinder[q + 1];
for (int i = 1; i <= q; i++) cylinders[i] = new Cylinder(in.nextInt(), in.nextInt(), in.nextInt());
for (int j = 0; j < n + 1; j++) {
for (int k = 0; k < m + 1; k++) {
dp[j][k] = Integer.MAX_VALUE / 2;
}
}
dp[0][0] = 0;
for (int i = 1; i < q + 1; i++) {
for (int j = n; j >= 0; j--) {
for (int k = m; k >= 0; k--) {
dp[j][k] = Math.min(dp[j][k],
dp[Math.max(0, j - cylinders[i].oxygen)][Math.max(0, k - cylinders[i].nitrogen)] + cylinders[i].weight
);
}
}
}
out.println(dp[n][m]);
out.flush();
out.close();
}
01背包的方案数
AcWing 278. 数字组合 原题链接
给定 NN 个正整数 A1,A2,…,ANA1,A2,…,AN,从中选出若干个数,使它们的和为 MM,求有多少种选择方案。
输入格式
第一行包含两个整数 NN 和 MM。
第二行包含 NN 个整数,表示 A1,A2,…,ANA1,A2,…,AN。
输出格式
包含一个整数,表示可选方案数。
数据范围
1≤N≤1001≤N≤100, 1≤M≤100001≤M≤10000, 1≤Ai≤10001≤Ai≤1000
输入样例:
4 4
1 1 2 2
输出样例:
3
题目思路

朴素写法:
private static void function1() {
int n = in.nextInt();
int m = in.nextInt();
int[] arr = new int[n + 1];
int[][] dp = new int[n + 1][m + 1];
for (int i = 1; i < n + 1; i++) arr[i] = in.nextInt();
for (int i = 0; i < n + 1; i++) dp[i][0] = 1;
for (int i = 1; i < n + 1; i++) {
for (int j = 0; j < m + 1; j++) {
dp[i][j] = dp[i - 1][j];
if (j >= arr[i]) {
dp[i][j] += dp[i - 1][j - arr[i]];
}
}
}
out.println(dp[n][m]);
out.flush();
out.close();
}
空间优化写法:
private static void function2() {
int n = in.nextInt();
int m = in.nextInt();
int[] arr = new int[n + 1];
int[] dp = new int[m + 1];
dp[0] = 1;
for (int i = 1; i < n + 1; i++) arr[i] = in.nextInt();
for (int i = 1; i < n + 1; i++) {
for (int j = m; j >= arr[i]; j--) {
dp[j] += dp[j - arr[i]];
}
}
out.println(dp[m]);
out.flush();
out.close();
}
完全背包求方案数
AcWing 1023. 买书 原题链接
小明手里有n元钱全部用来买书,书的价格为10元,20元,50元,100元。
问小明有多少种买书方案?(每种书可购买多本)
输入格式
一个整数 n,代表总共钱数。
输出格式
一个整数,代表选择方案种数。
数据范围
0≤n≤10000≤n≤1000
输入样例1:
20
输出样例1:
2
输入样例2:
15
输出样例2:
0
输入样例3:
0
输出样例3:
1
题目思路
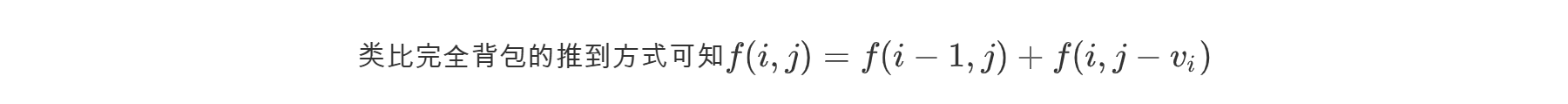
public static void main(String[] args) {
int n = in.nextInt();
int[] a = new int[]{0, 10, 20, 50, 100};
int[] dp = new int[n + 1];
dp[0] = 1;
for (int i = 1; i <= 4; i++) {
for (int j = a[i]; j < n + 1; j++) {
dp[j] += dp[j - a[i]];
}
}
out.println(dp[n]);
out.flush();
out.close();
}
