AcWing 1064. 小国王 原题链接
在 n×nn×n 的棋盘上放 kk 个国王,国王可攻击相邻的 88 个格子,求使它们无法互相攻击的方案总数。
输入格式
共一行,包含两个整数 nn 和 kk。
输出格式
共一行,表示方案总数,若不能够放置则输出00。
数据范围
1≤n≤101≤n≤10, 0≤k≤n20≤k≤n2
输入样例:
3 2
输出样例:
16
题目思路

private static int n;
private static int m;
private static int[] count;
private static List<Integer> legalState;
private static List<List<Integer>> legalTransfer;
//x二进制表示中1的个数
private static int countNumber(int x) {
int res = 0;
for (int i = 0; i < n; i++) {
res += (x >> i) & 1;
}
return res;
}
//判断状态是否合法,不能有相邻的1
private static boolean check(int state) {
for (int i = 0; i < n; i++) {
if (((state >> i) & 1) == 1 && ((state >> (i + 1)) & 1) == 1) {
return false;
}
}
return true;
}
private static void init() {
count = new int[1 << n];
legalState = new ArrayList<>();
legalTransfer = new ArrayList<>();
//找到所有合法状态
for (int i = 0; i < 1 << n; i++) {
if (check(i)) {
legalState.add(i);
count[i] = countNumber(i);
}
}
for (int i = 0; i < legalState.size(); i++) {
legalTransfer.add(new ArrayList<>());
}
//枚举所有合法状态,找到合法转移
for (int i = 0; i < legalState.size(); i++) {
for (int j = 0; j < legalState.size(); j++) {
int a = legalState.get(i);
int b = legalState.get(j);
if ((a & b) == 0 && check(a | b)) {
//存储的下标
legalTransfer.get(i).add(j);
}
}
}
}
public static void main(String[] args) {
n = in.nextInt();
m = in.nextInt();
init();
long[][][] dp = new long[n + 2][m + 1][1 << n];
//什么也不放算一种方案
dp[0][0][0] = 1;
//枚举到第i+1行
for (int i = 1; i <= n + 1; i++) {
for (int j = 0; j <= m; j++) {
//枚举第i行状态
for (int a = 0; a < legalState.size(); a++) {
int stateA = legalState.get(a);
//合法的第i-1行状态
for (int b : legalTransfer.get(a)) {
int stateB = legalState.get(b);
int c = count[stateB];
//国王数量不够
if (j < c) continue;
dp[i][j][stateA] += dp[i - 1][j - c][stateB];
}
}
}
}
out.println(dp[n + 1][m][0]);
out.flush();
out.close();
}
AcWing 327. 玉米田 原题链接
农夫约翰的土地由 M×NM×N 个小方格组成,现在他要在土地里种植玉米。
非常遗憾,部分土地是不育的,无法种植。
而且,相邻的土地不能同时种植玉米,也就是说种植玉米的所有方格之间都不会有公共边缘。
现在给定土地的大小,请你求出共有多少种种植方法。
土地上什么都不种也算一种方法。
输入格式
第 11 行包含两个整数 MM 和 NN。
第 2..M+12..M+1 行:每行包含 NN 个整数 00 或 11,用来描述整个土地的状况,11 表示该块土地肥沃,00 表示该块土地不育。
输出格式
输出总种植方法对 108108 取模后的值。
数据范围
1≤M,N≤121≤M,N≤12
输入样例:
2 3
1 1 1
0 1 0
输出样例:
9
题目思路

private static int n;
private static int m;
//用二进制表示地图
private static int[] map;
private static List<Integer> legalState;
private static List<List<Integer>> legalTransfer;
private static boolean check(int state) {
for (int i = 0; i < m; i++) {
if (((state >> i) & 1) == 1 && (state >> (i + 1) & 1) == 1) {
return false;
}
}
return true;
}
private static void init() {
legalState = new ArrayList<>();
legalTransfer = new ArrayList<>();
for (int i = 0; i < 1 << m; i++) {
if (check(i)) {
legalState.add(i);
}
}
for (int i = 0; i < legalState.size(); i++) legalTransfer.add(new ArrayList<>());
for (int i = 0; i < legalState.size(); i++) {
for (int j = 0; j < legalState.size(); j++) {
int a = legalState.get(i);
int b = legalState.get(j);
if ((a & b) == 0) {
legalTransfer.get(i).add(j);
}
}
}
}
public static void main(String[] args) {
n = in.nextInt();
m = in.nextInt();
map = new int[n + 2];
final int MOD = (int)1e8;
for (int i = 1; i <= n; i++) {
for (int j = 0; j < m; j++) {
int t = in.nextInt();
//如果t是0代表不能种植,把他存为这一位已经占用了即为1
map[i] += (t ^ 1) << j;
}
}
init();
int[][] dp = new int[n + 2][1 << m];
dp[0][0] = 1;
for (int i = 1; i <= n + 1; i++) {
for (int a = 0; a < legalState.size(); a++) {
int stateA = legalState.get(a);
for (int b : legalTransfer.get(a)) {
int stateB = legalState.get(b);
//种植到了不能种植的地方
if ((map[i] & stateA) != 0) continue;
dp[i][stateA] = (dp[i][stateA] + dp[i - 1][stateB]) % MOD;
}
}
}
out.println(dp[n + 1][0]);
out.flush();
out.close();
}
AcWing 292. 炮兵阵地 原题链接
司令部的将军们打算在 N×MN×M 的网格地图上部署他们的炮兵部队。
一个 N×MN×M 的地图由 NN 行 MM 列组成,地图的每一格可能是山地(用 H 表示),也可能是平原(用 P 表示),如下图。
在每一格平原地形上最多可以布置一支炮兵部队(山地上不能够部署炮兵部队);一支炮兵部队在地图上的攻击范围如图中黑色区域所示:
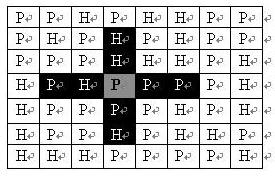
如果在地图中的灰色所标识的平原上部署一支炮兵部队,则图中的黑色的网格表示它能够攻击到的区域:沿横向左右各两格,沿纵向上下各两格。
图上其它白色网格均攻击不到。
从图上可见炮兵的攻击范围不受地形的影响。
现在,将军们规划如何部署炮兵部队,在防止误伤的前提下(保证任何两支炮兵部队之间不能互相攻击,即任何一支炮兵部队都不在其他支炮兵部队的攻击范围内),在整个地图区域内最多能够摆放多少我军的炮兵部队。
输入格式
第一行包含两个由空格分割开的正整数,分别表示 NN 和 MM;
接下来的 NN 行,每一行含有连续的 MM 个字符(P 或者 H),中间没有空格。按顺序表示地图中每一行的数据。
输出格式
仅一行,包含一个整数 KK,表示最多能摆放的炮兵部队的数量。
数据范围
N≤100,M≤10N≤100,M≤10
输入样例:
5 4
PHPP
PPHH
PPPP
PHPP
PHHP
输出样例:
6
题目思路

private static int n;
private static int m;
private static int[] map;
private static int[] count;
private static List<Integer> legalState;
private static int countNumber(int x) {
int res = 0;
for (int i = 0; i < m; i++) {
res += (x >> i) & 1;
}
return res;
}
private static boolean check(int state) {
for (int i = 0; i < m; i++) {
if (
((state >> i) & 1) == 1 && (((state >> (i + 1)) & 1) == 1 || ((state >> (i + 2)) & 1) == 1)
) {
return false;
}
}
return true;
}
private static void init() {
legalState = new ArrayList<>();
count = new int[1 << m];
for (int i = 0; i < 1 << m; i++) {
if (check(i)) {
legalState.add(i);
count[i] = countNumber(i);
}
}
}
public static void main(String[] args) {
n = in.nextInt();
m = in.nextInt();
map = new int[n + 3];
//用滚动数组进行优化
//i,i-1必然是一个奇数一个偶数
int[][][] dp = new int[2][1 << m][1 << m];
char[][] charArray = new char[n + 1][m];
for (int i = 1; i <= n; i++) {
String str = in.next();
System.arraycopy(str.toCharArray(), 0, charArray[i], 0, m);
}
for (int i = 1; i <= n; i++) {
for (int j = 0; j < m; j++) {
if (charArray[i][j] == 'H') {
map[i] += 1 << j;
}
}
}
init();
for (int i = 1; i <= n + 2; i++) {
for (int a = 0; a < legalState.size(); a++) {
int stateA = legalState.get(a);
for (int b = 0; b < legalState.size(); b++) {
int stateB = legalState.get(b);
for (int c = 0; c < legalState.size(); c++) {
int stateC = legalState.get(c);
//第i行和第i-1行有放在不能放的地方
if ((map[i] & stateA) != 0 || (map[i - 1] & stateB) != 0) {
continue;
}
//不能有邻边
if ((stateA & stateB) == 0 && (stateA & stateC) == 0 && (stateB & stateC) == 0) {
dp[i & 1][stateA][stateB] = Math.max(dp[i & 1][stateA][stateB], dp[(i - 1) & 1][stateB][stateC] + count[stateA]);
}
}
}
}
}
out.println(dp[(n + 2) & 1][0][0]);
out.flush();
out.close();
}
AcWing 524. 愤怒的小鸟 原题链接
Kiana 最近沉迷于一款神奇的游戏无法自拔。
简单来说,这款游戏是在一个平面上进行的。
有一架弹弓位于 (0,0)(0,0) 处,每次 Kiana 可以用它向第一象限发射一只红色的小鸟, 小鸟们的飞行轨迹均为形如 y=ax2+bxy=ax2+bx 的曲线,其中 a,ba,b 是 Kiana 指定的参数,且必须满足 a<0a<0。
当小鸟落回地面(即 xx 轴)时,它就会瞬间消失。
在游戏的某个关卡里,平面的第一象限中有 nn 只绿色的小猪,其中第 ii 只小猪所在的坐标为 (xi,yi)(xi,yi)。
如果某只小鸟的飞行轨迹经过了 (xi, yi)(xi, yi),那么第 ii 只小猪就会被消灭掉,同时小鸟将会沿着原先的轨迹继续飞行;
如果一只小鸟的飞行轨迹没有经过 (xi, yi)(xi, yi),那么这只小鸟飞行的全过程就不会对第 ii 只小猪产生任何影响。
例如,若两只小猪分别位于 (1,3)(1,3) 和 (3,3)(3,3),Kiana 可以选择发射一只飞行轨迹为 y=−x2+4xy=−x2+4x 的小鸟,这样两只小猪就会被这只小鸟一起消灭。
而这个游戏的目的,就是通过发射小鸟消灭所有的小猪。
这款神奇游戏的每个关卡对 Kiana 来说都很难,所以 Kiana 还输入了一些神秘的指令,使得自己能更轻松地完成这个这个游戏。
这些指令将在输入格式中详述。
假设这款游戏一共有 TT 个关卡,现在 Kiana 想知道,对于每一个关卡,至少需要发射多少只小鸟才能消灭所有的小猪。
由于她不会算,所以希望由你告诉她。
注意:本题除 NOIP 原数据外,还包含加强数据。
输入格式
第一行包含一个正整数 TT,表示游戏的关卡总数。
下面依次输入这 TT 个关卡的信息。
每个关卡第一行包含两个非负整数 n,mn,m,分别表示该关卡中的小猪数量和 Kiana 输入的神秘指令类型。
接下来的 nn 行中,第 ii 行包含两个正实数 (xi,yi)(xi,yi),表示第 ii 只小猪坐标为 (xi,yi)(xi,yi),数据保证同一个关卡中不存在两只坐标完全相同的小猪。
如果 m=0m=0,表示 Kiana 输入了一个没有任何作用的指令。
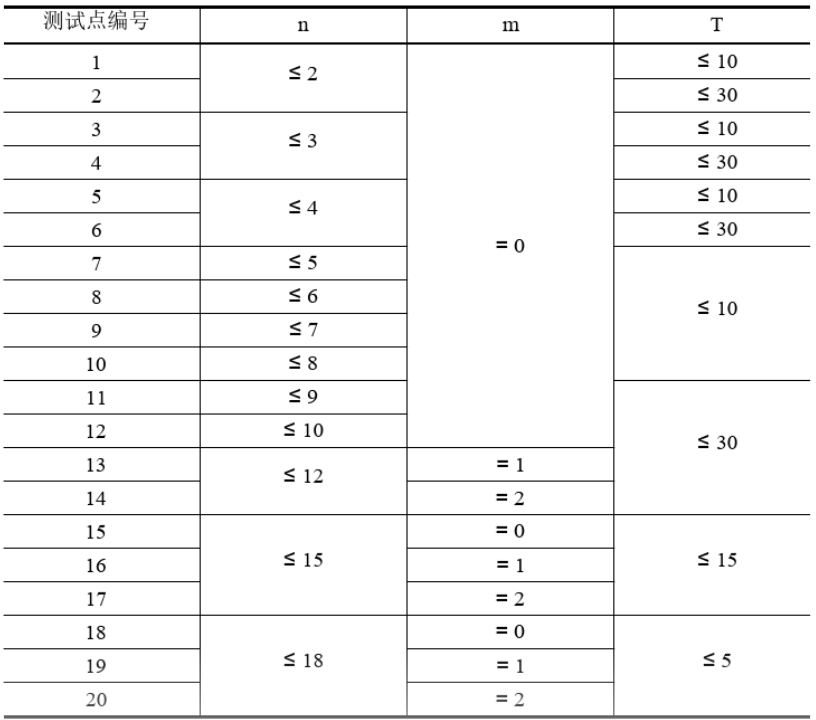
如果 m=1m=1,则这个关卡将会满足:至多用 ⌈n/3+1⌉⌈n/3+1⌉ 只小鸟即可消灭所有小猪。
如果 m=2m=2,则这个关卡将会满足:一定存在一种最优解,其中有一只小鸟消灭了至少 ⌊n/3⌋⌊n/3⌋ 只小猪。
保证 1≤n≤18,0≤m≤2,0<xi,yi<101≤n≤18,0≤m≤2,0<xi,yi<10,输入中的实数均保留到小数点后两位。
上文中,符号 ⌈c⌉⌈c⌉ 和 ⌊c⌋⌊c⌋ 分别表示对 cc 向上取整和向下取整,例如 :⌈2.1⌉=⌈2.9⌉=⌈3.0⌉=⌊3.0⌋=⌊3.1⌋=⌊3.9⌋=3⌈2.1⌉=⌈2.9⌉=⌈3.0⌉=⌊3.0⌋=⌊3.1⌋=⌊3.9⌋=3。
输出格式
对每个关卡依次输出一行答案。
输出的每一行包含一个正整数,表示相应的关卡中,消灭所有小猪最少需要的小鸟数量。
数据范围
输入样例:
2
2 0
1.00 3.00
3.00 3.00
5 2
1.00 5.00
2.00 8.00
3.00 9.00
4.00 8.00
5.00 5.00
输出样例:
1
1
题目思路

private static int n;
private static int m;
private static int[][] path;
private static Bird[] birds;
private static final double EPS = 1e-8;
private static int compare(double a, double b) {
if (Math.abs(a - b) <= 1e-8) return 0;
if (a > b) return 1;
return -1;
}
private static class Bird {
private double x;
private double y;
public Bird(double x, double y) {
this.x = x;
this.y = y;
}
}
private static void initPath() {
//存储两个点所组成的抛物线,能够覆盖的情况二进制表示
path = new int[n][n];
for (int i = 0; i < n; i++) {
//这条线一定可以覆盖自己
//能够处理只有一个点的情况
path[i][i] = 1 << i;
for (int j = 0; j < n; j++) {
double x1 = birds[i].x;
double x2 = birds[j].x;
double y1 = birds[i].y;
double y2 = birds[j].y;
//x1 != x2
if (compare(x1, x2) == 0) continue;
double a = (y1 / x1 - y2 / x2) / (x1 - x2);
double b = y1 / x1 - a * x1;
// a要<0
if (compare(a, 0D) >= 0) continue;
int state = 0;
//看这条抛物线能够穿过哪些点
for (int k = 0; k < n; k++) {
double x = birds[k].x;
double y = birds[k].y;
if (compare(a * x * x + b * x, y) == 0) {
state += 1 << k;
}
}
path[i][j] = state;
}
}
}
public static void main(String[] args) {
int t = in.nextInt();
while (t-- > 0) {
n = in.nextInt();
m = in.nextInt();
int[] dp = new int[1 << n];
Arrays.fill(dp, Integer.MAX_VALUE / 2);
//状态为0时,不需要抛物线
dp[0] = 0;
birds = new Bird[n];
for (int i = 0; i < n; i++) birds[i] = new Bird(in.nextDouble(), in.nextDouble());
initPath();
//i == (1 << n) - 1时就已经全部打到了
for (int i = 0; i < 1 << n; i++) {
int x = -1;
for (int j = 0; j < n; j++) {
//找到一个没有被打到的点
if (((i >> j) & 1) == 0) {
x = j;
break;
}
}
//全是1的情况
if (x == -1) {
break;
}
//枚举所有经过x的抛物线
for (int j = 0; j < n; j++) {
// (i | path[x][j])就是选择这条抛物线之后的new_state
// 此时状态i可以在选择这条抛物线时更新new_state的状态
dp[i | path[x][j]] = Math.min(dp[i | path[x][j]], dp[i] + 1);
}
}
//有n只小猪没有被打
out.println(dp[(1 << n) - 1]);
}
out.flush();
out.close();
}
