高斯消元

算法步骤
- 枚举每一列
c- 找到当前这一列中绝对值最大的一行
- 将这行换到最上面行(
i)的位置,(第一次最上面行就是第一行) - 将该行第一个数变成
1,即所在行的数除以同一个数 - 将下面所有行的第
c列消成0,即列元素所在行同时加减某个数 - 此时第
c列以及最上面的行已固定,继续枚举后面的列,最上面的行更新成(i+1)
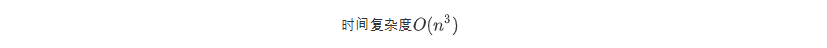
AcWing 883. 高斯消元解线性方程组 原题链接
输入一个包含n个方程n个未知数的线性方程组。
方程组中的系数为实数。
求解这个方程组。
下图为一个包含m个方程n个未知数的线性方程组示例:
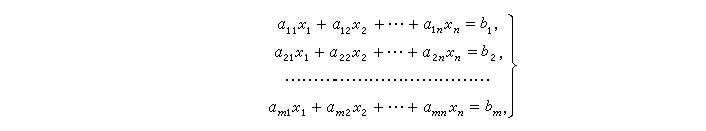
输入格式
第一行包含整数n。
接下来n行,每行包含n+1个实数,表示一个方程的n个系数以及等号右侧的常数。
输出格式
如果给定线性方程组存在唯一解,则输出共n行,其中第i行输出第i个未知数的解,结果保留两位小数。
如果给定线性方程组存在无数解,则输出“Infinite group solutions”。
如果给定线性方程组无解,则输出“No solution”。
数据范围
1≤n≤1001≤n≤100, 所有输入系数以及常数均保留两位小数,绝对值均不超过100。
输入样例:
3
1.00 2.00 -1.00 -6.00
2.00 1.00 -3.00 -9.00
-1.00 -1.00 2.00 7.00
输出样例:
1.00
-2.00
3.00
private static class Gauss {
private final double[][] det;
public Gauss(double[][] det) {
this.det = det;
}
public int gauss() {
int c,r;
int n = det.length;
double EPS = 1e-6;
for (c = 0, r = 0; c < n; c++) {
int t = r;
for (int i = r; i < n; i++) {
if (Math.abs(det[i][c]) > Math.abs(det[t][c])) {
t = i;
}
}
//当前这一列为0
if (Math.abs(det[t][c]) <= EPS) continue;
for (int i = c; i <= n; i++) {
double temp = det[t][i];
det[t][i] = det[r][i];
det[r][i] = temp;
}
for (int i = n; i >= c; i--) {
det[r][i] /= det[r][c];
}
for (int i = r + 1; i < n; i++) {
if (Math.abs(det[i][c]) > EPS) {
for (int j = n; j >= c; j--) {
det[i][j] -= det[r][j] * det[i][c];
}
}
}
r++;
}
if (r < n) {
for (int i = r; i < n; i++) {
//出现 0 = 非0
if (Math.abs(det[i][n]) > EPS) {
//无解
return 2;
}
}
//无穷多组解
return 1;
}
//倒着把解求出来
for (int i = n - 1; i >= 0; i--) {
for (int j = i + 1; j < n; j++) {
det[i][n] -= det[i][j] * det[j][n];
}
}
//唯一解
return 0;
}
}
public static void main(String[] args) {
int n = in.nextInt();
double[][] a = new double[n][n + 1];
for (int i = 0; i < n; i++) {
for (int j = 0; j < n + 1; j++) {
a[i][j] = in.nextDouble();
}
}
Gauss gauss = new Gauss(a);
int res = gauss.gauss();
if (res == 0) {
for (int i = 0; i < n; i++) {
out.printf("%.2f\n", a[i][n]);
}
} else if (res == 1) {
out.println("Infinite group solutions");
} else if (res == 2) {
out.println("No solution");
}
out.flush();
out.close();
}
AcWing 884. 高斯消元解异或线性方程组 原题链接
输入一个包含n个方程n个未知数的异或线性方程组。
方程组中的系数和常数为0或1,每个未知数的取值也为0或1。
求解这个方程组。
异或线性方程组示例如下:
M[1][1]x[1] ^ M[1][2]x[2] ^ … ^ M[1][n]x[n] = B[1]
M[2][1]x[1] ^ M[2][2]x[2] ^ … ^ M[2][n]x[n] = B[2]
…
M[n][1]x[1] ^ M[n][2]x[2] ^ … ^ M[n][n]x[n] = B[n]
其中“^”表示异或(XOR),M[i][j]表示第i个式子中x[j]的系数,B[i]是第i个方程右端的常数,取值均为0或1。
输入格式
第一行包含整数n。
接下来n行,每行包含n+1个整数0或1,表示一个方程的n个系数以及等号右侧的常数。
输出格式
如果给定线性方程组存在唯一解,则输出共n行,其中第i行输出第i个未知数的解。
如果给定线性方程组存在多组解,则输出“Multiple sets of solutions”。
如果给定线性方程组无解,则输出“No solution”。
数据范围
1≤n≤1001≤n≤100
输入样例:
3
1 1 0 1
0 1 1 0
1 0 0 1
输出样例:
1
0
0
private static class Gauss {
private final int[][] det;
public Gauss(int[][] det) {
this.det = det;
}
public int gauss() {
int c,r;
int n = det.length;
for (c = 0, r = 0; c < n; c++) {
int t = r;
for (int i = r; i < n; i++) {
if (det[i][c] > 0) {
t = i;
break;
}
}
if (det[t][c] == 0) continue;
for (int i = c; i <= n; i++) {
int temp = det[t][i];
det[t][i] = det[r][i];
det[r][i] = temp;
}
for (int i = r + 1; i < n; i++) {
if (det[i][c] != 0) {
for (int j = n; j >= c; j--) {
det[i][j] ^= det[r][j];
}
}
}
r++;
}
if (r < n) {
for (int i = r; i < n; i++) {
//出现 0 = 非0
if (det[i][n] != 0) {
//无解
return 2;
}
}
//无穷多组解
return 1;
}
//倒着把解求出来
for (int i = n - 1; i >= 0; i--) {
for (int j = i + 1; j < n; j++) {
det[i][n] ^= det[i][j] & det[j][n];
}
}
//唯一解
return 0;
}
}
public static void main(String[] args) {
int n = in.nextInt();
int[][] a = new int[n][n + 1];
for (int i = 0; i < n; i++) {
for (int j = 0; j < n + 1; j++) {
a[i][j] = in.nextInt();
}
}
Gauss gauss = new Gauss(a);
int res = gauss.gauss();
if (res == 0) {
for (int i = 0; i < n; i++) {
out.println(a[i][n]);
}
} else if (res == 1) {
out.println("Multiple sets of solutions");
} else if (res == 2) {
out.println("No solution");
}
out.flush();
out.close();
}
