组合数

根据数据量选择合适的方式

卡特兰数

组合恒等式

AcWing 885. 求组合数 I 原题链接
给定nn组询问,每组询问给定两个整数a,ba,b,请你输出Cba mod (109+7)Cab mod (109+7)的值。
输入格式
第一行包含整数nn。
接下来nn行,每行包含一组aa和bb。
输出格式
共nn行,每行输出一个询问的解。
数据范围
1≤n≤100001≤n≤10000, 1≤b≤a≤20001≤b≤a≤2000
输入样例:
3
3 1
5 3
2 2
输出样例:
3
10
1
private static class Combination{
private int[][] c;
private final int n;
public Combination(int n) {
this.n = n;
init();
}
private void init(){
c = new int[n + 1][n + 1];
for (int i = 0; i <= n; i++) {
for (int j = 0; j <= i; j++) {
int MOD = (int) (1e9 + 7);
if (j == 0) c[i][j] = 1;
else c[i][j] = (c[i - 1][j] + c[i - 1][j - 1]) % MOD;
}
}
}
public int com(int a, int b) {
return c[a][b];
}
}
AcWing 886. 求组合数 II 原题链接
给定nn组询问,每组询问给定两个整数a,ba,b,请你输出Cba mod (109+7)Cab mod (109+7)的值。
输入格式
第一行包含整数nn。
接下来nn行,每行包含一组aa和bb。
输出格式
共nn行,每行输出一个询问的解。
数据范围
1≤n≤100001≤n≤10000, 1≤b≤a≤1051≤b≤a≤105
输入样例:
3
3 1
5 3
2 2
输出样例:
3
10
1
private static class Combination {
private long[] fact;
private long[] inFact;
private final int n;
private final int MOD = (int) (1e9 + 7);
private int fastPower(long a, long b, long q) {
long res = 1L;
while (b > 0) {
if ((b & 1) == 1) {
res = res * a % q;
}
b >>= 1;
a = a * a % q;
}
return (int) res;
}
public Combination(int n) {
this.n = n;
init();
}
private void init() {
fact = new long[n];
inFact = new long[n];
fact[0] = inFact[0] = 1;
for (int i = 1; i < n; i++) {
fact[i] = fact[i - 1] * i % MOD;
inFact[i] = inFact[i - 1] * fastPower(i, MOD - 2, MOD) % MOD;
}
}
public int com(int a, int b) {
return (int)(fact[a] * inFact[b] % MOD * inFact[a - b] % MOD);
}
}
AcWing 887. 求组合数 III 原题链接
给定nn组询问,每组询问给定三个整数a,b,pa,b,p,其中pp是质数,请你输出Cba mod pCab mod p的值。
输入格式
第一行包含整数nn。
接下来nn行,每行包含一组a,b,pa,b,p。
输出格式
共nn行,每行输出一个询问的解。
数据范围
1≤n≤201≤n≤20, 1≤b≤a≤10181≤b≤a≤1018, 1≤p≤1051≤p≤105,
输入样例:
3
5 3 7
3 1 5
6 4 13
输出样例:
3
3
2
private static class Combination {
private int mod;
public void setMod(int mod) {
this.mod = mod;
}
public Combination() {
}
private int fastPower(long a, long b, long q) {
long res = 1L;
while (b > 0) {
if ((b & 1) == 1) {
res = res * a % q;
}
b >>= 1;
a = a * a % q;
}
return (int) res;
}
private long com(int a, int b) {
long res = 1L;
for (int i = 1, j = a; i <= b; i++, j--) {
res = res * j % mod;
res = res * fastPower(i, mod - 2, mod) % mod;
}
return (int) res;
}
public int lucas(long a, long b) {
if (a < mod && b < mod) {
return (int) com((int)a, (int)b);
}
return (int) (com((int)(a % mod), (int)(b % mod)) * lucas(a / mod, b / mod) % mod);
}
}
AcWing 888. 求组合数 IV 原题链接
输入a,ba,b,求CbaCab的值。
注意结果可能很大,需要使用高精度计算。
输入格式
共一行,包含两个整数aa和bb。
输出格式
共一行,输出CbaCab的值。
数据范围
1≤b≤a≤50001≤b≤a≤5000
输入样例:
5 3
输出样例:
10
private static class Combination{
private int[] primes;
private int[] sum;
private int count;
private boolean[] st;
private String com(int a, int b) {
initPrimes(a);
initSum(a, b);
BigInteger res = new BigInteger("1");
for (int i = 0; i < count; i++) {
for (int j = 0; j < sum[i]; j++) {
res = res.multiply(BigInteger.valueOf(primes[i]));
}
}
return res.toString();
}
private void initPrimes(int n){
primes = new int[n + 1];
st = new boolean[n + 1];
for (int i = 2; i <= n; i++) {
if (!st[i]) primes[count++] = i;
for (int j = 0; primes[j] <= n / i; j++) {
st[primes[j] * i] = true;
if (i % primes[j] == 0) break;
}
}
}
private void initSum(int a, int b) {
sum = new int[count];
for (int i = 0; i < count; i++) {
int p = primes[i];
sum[i] = getNumber(a, p) - getNumber(b, p) - getNumber(a - b, p);
}
}
//得到n中质因子p的个数
private int getNumber(int n, int p) {
int res = 0;
while (n > 0) {
res += n / p;
n /= p;
}
return res;
}
}
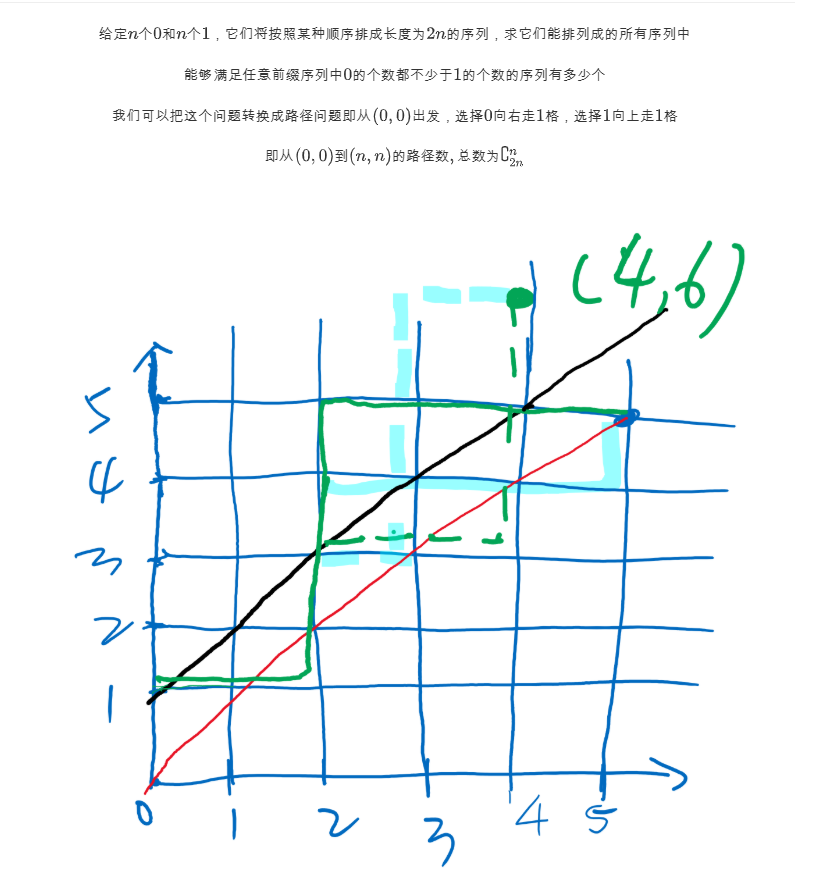
AcWing 889. 满足条件的01序列 原题链接
给定nn个00和nn个11,它们将按照某种顺序排成长度为2n2n的序列,求它们能排列成的所有序列中,能够满足任意前缀序列中00的个数都不少于11的个数的序列有多少个。
输出的答案对109+7109+7取模。
输入格式
共一行,包含整数nn。
输出格式
共一行,包含一个整数,表示答案。
数据范围
1≤n≤1051≤n≤105
输入样例:
3
输出样例:
5
private static class Combination {
private long[] fact;
private long[] inFact;
private final int n;
private final int MOD = (int) (1e9 + 7);
private int fastPower(long a, long b, long q) {
long res = 1L;
while (b > 0) {
if ((b & 1) == 1) {
res = res * a % q;
}
b >>= 1;
a = a * a % q;
}
return (int) res;
}
public Combination(int n) {
this.n = n;
init();
}
private void init() {
fact = new long[n];
inFact = new long[n];
fact[0] = inFact[0] = 1;
for (int i = 1; i < n; i++) {
fact[i] = fact[i - 1] * i % MOD;
inFact[i] = inFact[i - 1] * fastPower(i, MOD - 2, MOD) % MOD;
}
}
public int com(int a, int b) {
return (int)(fact[a] * inFact[b] % MOD * inFact[a - b] % MOD);
}
}
public static void main(String[] args) {
int n = in.nextInt();
Combination c = new Combination(n << 1 + 5);
// /(n+1) = *(n+1)^{-1}
int res = (int) ((long)c.com(n << 1, n) * c.fastPower(n + 1, c.MOD - 2, c.MOD) % c.MOD);
out.println(res);
out.flush();
out.close();
}
