公平组合游戏ICG
若一个游戏满足
- 由两名玩家交替行动
- 在游戏进程的任意时刻,可以执行的合法行动与轮到哪名玩家无关(游戏的局势不能区分玩家的身份,例如黑白棋就是不行的)
- 不能行动的玩家判负
两种状态
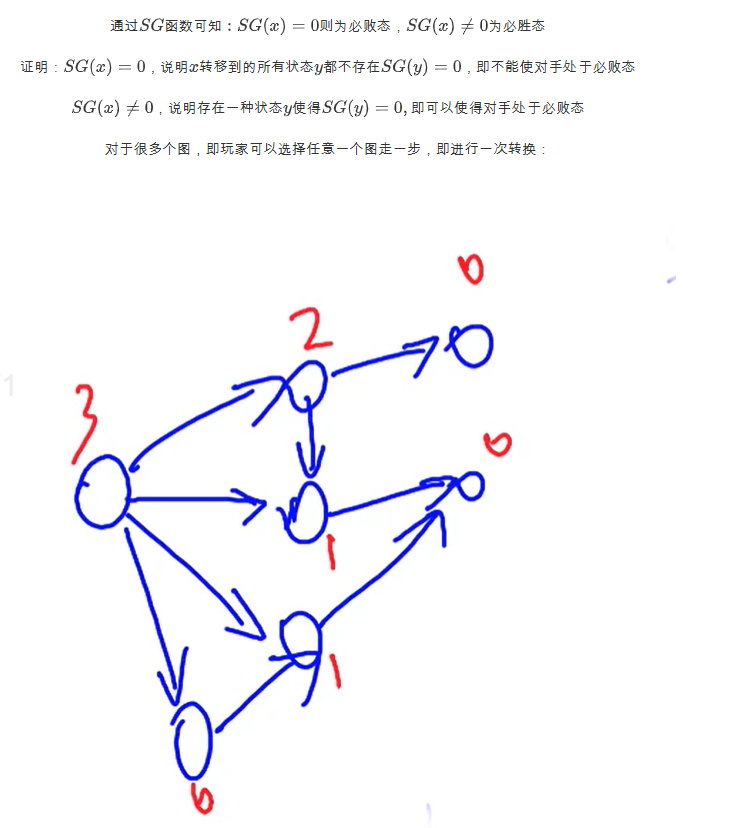
先手必败状态:不管怎么操作,剩下的状态都是先手必胜状态
先手必胜状态 :存在一种操作可以将状态转成先手必败状态
Nim游戏

结论

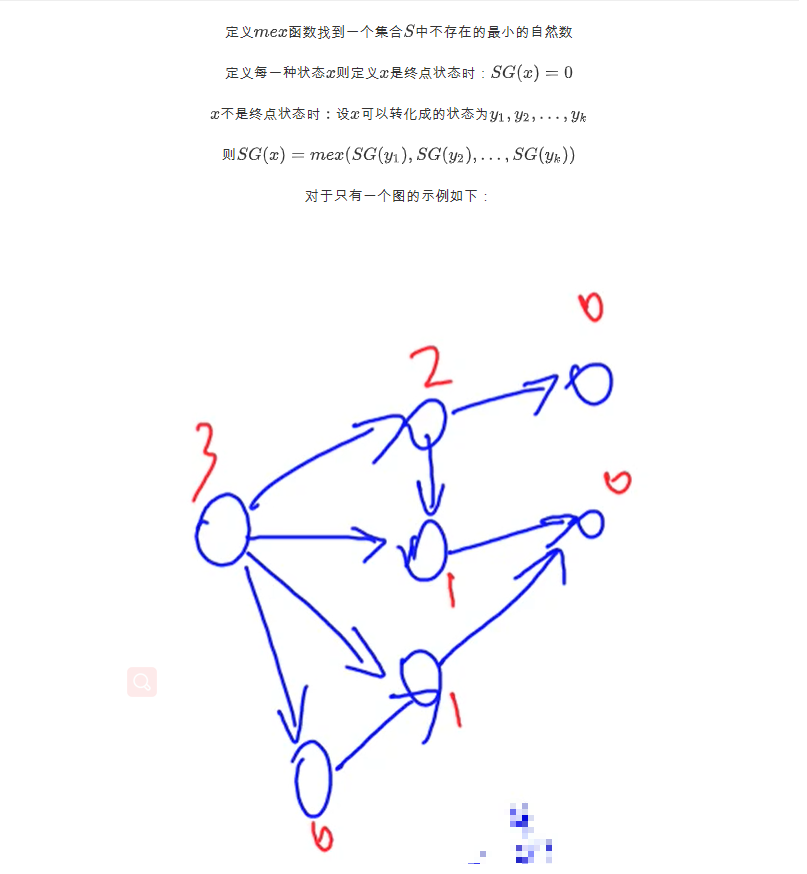
SG函数
AcWing 891. Nim游戏 原题链接
给定nn堆石子,两位玩家轮流操作,每次操作可以从任意一堆石子中拿走任意数量的石子(可以拿完,但不能不拿),最后无法进行操作的人视为失败。
问如果两人都采用最优策略,先手是否必胜。
输入格式
第一行包含整数nn。
第二行包含nn个数字,其中第 ii 个数字表示第 ii 堆石子的数量。
输出格式
如果先手方必胜,则输出“Yes”。
否则,输出“No”。
数据范围
1≤n≤1051≤n≤105, 1≤每堆石子数≤1091≤每堆石子数≤109
输入样例:
2
2 3
输出样例:
Yes
public static void main(String[] args) {
int n = in.nextInt();
int res = 0;
while (n-- > 0) {
res ^= in.nextInt();
}
if (res == 0) {
out.println("No");
}else {
out.println("Yes");
}
out.flush();
out.close();
}
AcWing 892. 台阶-Nim游戏 原题链接
现在,有一个nn级台阶的楼梯,每级台阶上都有若干个石子,其中第ii级台阶上有aiai个石子(i≥1i≥1)。
两位玩家轮流操作,每次操作可以从任意一级台阶上拿若干个石子放到下一级台阶中(不能不拿)。
已经拿到地面上的石子不能再拿,最后无法进行操作的人视为失败。
问如果两人都采用最优策略,先手是否必胜。
输入格式
第一行包含整数nn。
第二行包含nn个整数,其中第ii个整数表示第ii级台阶上的石子数aiai。
输出格式
如果先手方必胜,则输出“Yes”。
否则,输出“No”。
数据范围
1≤n≤1051≤n≤105, 1≤ai≤1091≤ai≤109
输入样例:
3
2 1 3
输出样例:
Yes
算法思路

public static void main(String[] args) {
int n = in.nextInt();
int res = 0;
for (int i = 1; i <= n; i++) {
int x = in.nextInt();
if ((i & 1) == 1) {
res ^= x;
}
}
if (res != 0) {
out.println("Yes");
}else {
out.println("No");
}
out.flush();
out.close();
}
AcWing 893. 集合-Nim游戏 原题链接
给定nn堆石子以及一个由kk个不同正整数构成的数字集合SS。
现在有两位玩家轮流操作,每次操作可以从任意一堆石子中拿取石子,每次拿取的石子数量必须包含于集合SS,最后无法进行操作的人视为失败。
问如果两人都采用最优策略,先手是否必胜。
输入格式
第一行包含整数kk,表示数字集合SS中数字的个数。
第二行包含kk个整数,其中第ii个整数表示数字集合SS中的第ii个数sisi。
第三行包含整数nn。
第四行包含nn个整数,其中第ii个整数表示第ii堆石子的数量hihi。
输出格式
如果先手方必胜,则输出“Yes”。
否则,输出“No”。
数据范围
1≤n,k≤1001≤n,k≤100, 1≤si,hi≤100001≤si,hi≤10000
输入样例:
2
2 5
3
2 4 7
输出样例:
Yes
算法思路
假设某堆石子的个数为10,可以求出它的初始状态SG(10)=1如图:
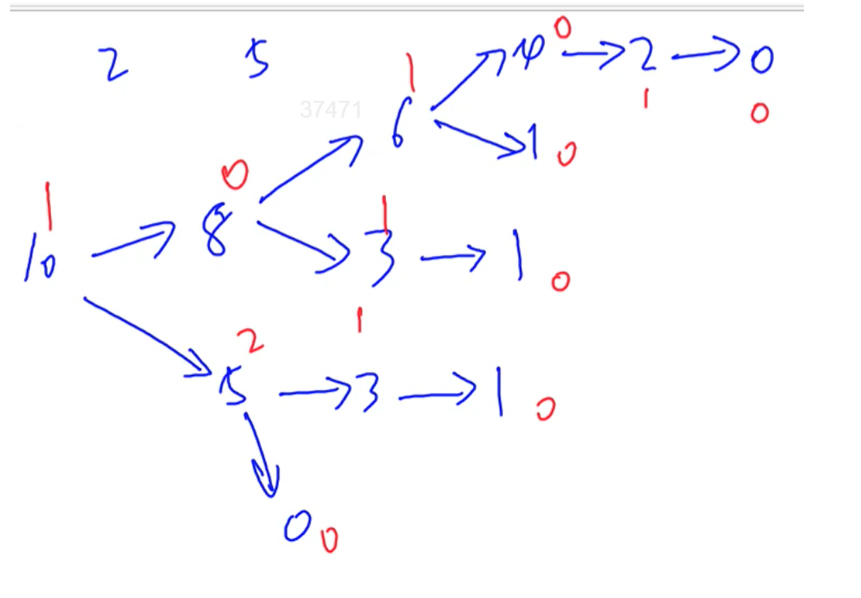 有
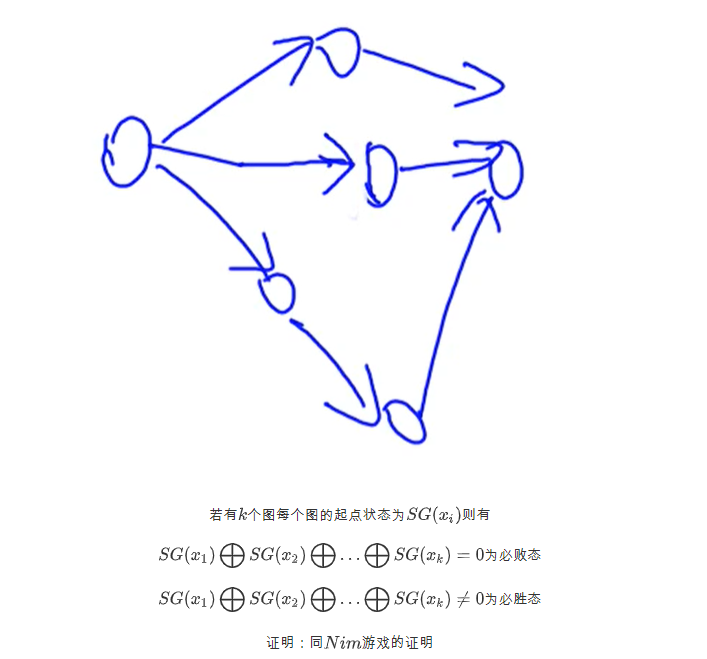
有n堆石子就能求出n个SG的初始值,将这些数进行异或即可得到整个问题的SG初始值
private static class SG {
//可以取的个数的集合
private int[] collection;
//sg函数的值
private int[] sg;
//石子个数集合
private int[] stoneNumber;
private final int N;
public SG(int N, int[] collection, int[] stoneNumber) {
this.collection = collection;
this.stoneNumber = stoneNumber;
this.N = N;
this.sg = new int[N];
Arrays.fill(sg, -1);
}
public int getXor() {
int res = 0;
for (int x : stoneNumber) {
res ^= sgFunction(x);
}
return res;
}
//记忆化搜索过程
private int sgFunction(int x) {
//状态已经被算过
if (sg[x] != -1) {
return sg[x];
}
//存储当前状态所有可以到达的状态
Set<Integer> set = new HashSet<>();
for (int out : collection) {
if (x >= out) {
set.add(sgFunction(x - out));
}
}
//求出当前集合不存在的最小自然数
for (int i = 0; ; i++) {
if (!set.contains(i)) {
sg[x] = i;
return i;
}
}
}
}
public static void main(String[] args) {
int n = in.nextInt();
int[] collection = new int[n];
for (int i = 0; i < n; i++) {
collection[i] = in.nextInt();
}
int m = in.nextInt();
int[] tones = new int[m];
for (int i = 0; i < m; i++) {
tones[i] = in.nextInt();
}
int max = -1;
for (int x : tones) {
max = Math.max(max, x);
}
SG sg = new SG(max + 1, collection, tones);
int res = sg.getXor();
if (res != 0) {
out.println("Yes");
}else {
out.println("No");
}
out.flush();
out.close();
}
AcWing 894. 拆分-Nim游戏 原题链接
给定nn堆石子,两位玩家轮流操作,每次操作可以取走其中的一堆石子,然后放入两堆规模更小的石子(新堆规模可以为0,且两个新堆的石子总数可以大于取走的那堆石子数),最后无法进行操作的人视为失败。
问如果两人都采用最优策略,先手是否必胜。
输入格式
第一行包含整数nn。
第二行包含nn个整数,其中第ii个整数表示第ii堆石子的数量aiai。
输出格式
如果先手方必胜,则输出“Yes”。
否则,输出“No”。
数据范围
1≤n,ai≤1001≤n,ai≤100
输入样例:
2
2 3
输出样例:
Yes
算法思路

private static class SG {
//sg函数的值
private int[] sg;
//石子个数集合
private int[] stoneNumber;
private final int N;
public SG(int N, int[] stoneNumber) {
this.stoneNumber = stoneNumber;
this.N = N;
this.sg = new int[N];
Arrays.fill(sg, -1);
}
public int getXor() {
int res = 0;
for (int x : stoneNumber) {
res ^= sgFunction(x);
}
return res;
}
//记忆化搜索过程
private int sgFunction(int x) {
//状态已经被算过
if (sg[x] != -1) {
return sg[x];
}
//存储当前状态所有可以到达的状态
Set<Integer> set = new HashSet<>();
for (int i = 0; i < x; i++) {
for (int j = 0; j <= i; j++) {
set.add(sgFunction(i) ^ sgFunction(j));
}
}
int number = mex(set);
sg[x] = number;
return number;
}
//mex函数
//求出当前集合不存在的最小自然数
private int mex(Set<Integer> set) {
for (int i = 0; ; i++) {
if (!set.contains(i)) {
return i;
}
}
}
}
public static void main(String[] args) {
int n = in.nextInt();
int[] stones = new int[n];
in.nextIntegerArray(stones);
int max = -1;
for (int x : stones) max = Math.max(max, x);
SG sg = new SG(max + 1, stones);
int res = sg.getXor();
if (res != 0) {
out.println("Yes");
}else {
out.println("No");
}
out.flush();
out.close();
}
