数字三角形模型
AcWing 1015. 摘花生 原题链接
Hello Kitty想摘点花生送给她喜欢的米老鼠。
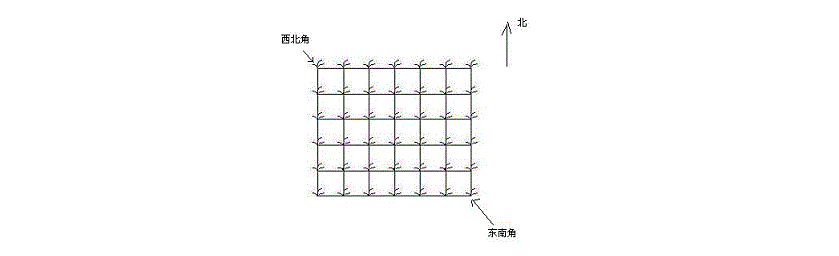
她来到一片有网格状道路的矩形花生地(如下图),从西北角进去,东南角出来。
地里每个道路的交叉点上都有种着一株花生苗,上面有若干颗花生,经过一株花生苗就能摘走该它上面所有的花生。
Hello Kitty只能向东或向南走,不能向西或向北走。
问Hello Kitty最多能够摘到多少颗花生。
输入格式
第一行是一个整数T,代表一共有多少组数据。
接下来是T组数据。
每组数据的第一行是两个整数,分别代表花生苗的行数R和列数 C。
每组数据的接下来R行数据,从北向南依次描述每行花生苗的情况。每行数据有C个整数,按从西向东的顺序描述了该行每株花生苗上的花生数目M。
输出格式
对每组输入数据,输出一行,内容为Hello Kitty能摘到得最多的花生颗数。
数据范围
1≤T≤1001≤T≤100, 1≤R,C≤1001≤R,C≤100, 0≤M≤10000≤M≤1000
输入样例:
2
2 2
1 1
3 4
2 3
2 3 4
1 6 5
输出样例:
8
16
题目思路

public static void main(String[] args) {
int m = in.nextInt();
while (m-- > 0) {
int row = in.nextInt();
int col = in.nextInt();
int[][] arr = new int[row][col];
for (int i = 0; i < row; i++) {
for (int j = 0; j < col; j++) {
arr[i][j] = in.nextInt();
}
}
int[][] dp = new int[row + 1][col + 1];
for (int i = 1; i < row + 1; i++) {
for (int j = 1; j < col + 1; j++) {
dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]) + arr[i - 1][j - 1];
}
}
out.println(dp[row][col]);
}
out.flush();
out.close();
}
AcWing 1018. 最低通行费 原题链接
一个商人穿过一个N×N的正方形的网格,去参加一个非常重要的商务活动。
他要从网格的左上角进,右下角出。
每穿越中间1个小方格,都要花费1个单位时间。
商人必须在(2N-1)个单位时间穿越出去。
而在经过中间的每个小方格时,都需要缴纳一定的费用。
这个商人期望在规定时间内用最少费用穿越出去。
请问至少需要多少费用?
注意:不能对角穿越各个小方格(即,只能向上下左右四个方向移动且不能离开网格)。
输入格式
第一行是一个整数,表示正方形的宽度N。
后面N行,每行N个不大于100的整数,为网格上每个小方格的费用。
输出格式
输出一个整数,表示至少需要的费用。
数据范围
1≤N≤1001≤N≤100
输入样例:
5
1 4 6 8 10
2 5 7 15 17
6 8 9 18 20
10 11 12 19 21
20 23 25 29 33
输出样例:
109
样例解释
样例中,最小值为109=1+2+5+7+9+12+19+21+33。
题目思路

public static void main(String[] args) {
int n = in.nextInt();
int[][] arr = new int[n][n];
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
arr[i][j] = in.nextInt();
}
}
int[][] dp = new int[n + 1][n + 1];
for (int i = 0; i < n + 1; i++) {
Arrays.fill(dp[i], Integer.MAX_VALUE);
}
dp[0][1] = dp[1][0] = 0;
for (int i = 1; i < n + 1; i++) {
for (int j = 1; j < n + 1; j++) {
dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - 1]) + arr[i - 1][j - 1];
}
}
out.println(dp[n][n]);
out.flush();
out.close();
}
AcWing 1027. 方格取数 原题链接
设有 N×N 的方格图,我们在其中的某些方格中填入正整数,而其它的方格中则放入数字0。如下图所示:
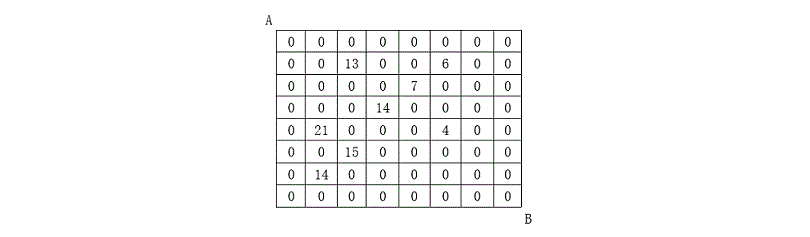
某人从图中的左上角 A 出发,可以向下行走,也可以向右行走,直到到达右下角的 B 点。
在走过的路上,他可以取走方格中的数(取走后的方格中将变为数字0)。
此人从 A 点到 B 点共走了两次,试找出两条这样的路径,使得取得的数字和为最大。
输入格式
第一行为一个整数N,表示 N×N 的方格图。
接下来的每行有三个整数,第一个为行号数,第二个为列号数,第三个为在该行、该列上所放的数。
行和列编号从 11 开始。
一行“0 0 0”表示结束。
输出格式
输出一个整数,表示两条路径上取得的最大的和。
数据范围
N≤10N≤10
输入样例:
8
2 3 13
2 6 6
3 5 7
4 4 14
5 2 21
5 6 4
6 3 15
7 2 14
0 0 0
输出样例:
67
题目思路
与题目AcWing 1015. 摘花生 原题链接,区别就是要走两次

public static void main(String[] args) {
int n = in.nextInt();
int[][] arr = new int[n + 1][n + 1];
int row;
int col;
int val;
row = in.nextInt();col = in.nextInt();val = in.nextInt();
while (row != 0 || col != 0 || val != 0) {
arr[row][col] = val;
row = in.nextInt();col = in.nextInt();val = in.nextInt();
}
int[][][] dp = new int[2 * n + 1][n + 1][n + 1];
for (int k = 2; k < 2 * n + 1; k++) {
for (int i = 1; i < n + 1; i++) {
for (int i2 = 1; i2 < n + 1; i2++) {
int j = k - i;
int j2 = k - i2;
if (j >= 1 && j <= n && j2 >= 1 && j2 <= n) {
int add = arr[i][j];
if (i != i2) add += arr[i2][j2];
dp[k][i][i2] = Math.max(dp[k][i][i2], dp[k - 1][i - 1][i2 - 1] + add);
dp[k][i][i2] = Math.max(dp[k][i][i2], dp[k - 1][i][i2 - 1] + add);
dp[k][i][i2] = Math.max(dp[k][i][i2], dp[k - 1][i - 1][i2] + add);
dp[k][i][i2] = Math.max(dp[k][i][i2], dp[k - 1][i][i2] + add);
}
}
}
}
out.println(dp[2 * n][n][n]);
out.flush();
out.close();
}
AcWing 275. 传纸条 原题链接
小渊和小轩是好朋友也是同班同学,他们在一起总有谈不完的话题。
一次素质拓展活动中,班上同学安排坐成一个 mm 行 nn 列的矩阵,而小渊和小轩被安排在矩阵对角线的两端,因此,他们就无法直接交谈了。
幸运的是,他们可以通过传纸条来进行交流。
纸条要经由许多同学传到对方手里,小渊坐在矩阵的左上角,坐标(1,1),小轩坐在矩阵的右下角,坐标(m,n)。
从小渊传到小轩的纸条只可以向下或者向右传递,从小轩传给小渊的纸条只可以向上或者向左传递。
在活动进行中,小渊希望给小轩传递一张纸条,同时希望小轩给他回复。
班里每个同学都可以帮他们传递,但只会帮他们一次,也就是说如果此人在小渊递给小轩纸条的时候帮忙,那么在小轩递给小渊的时候就不会再帮忙,反之亦然。
还有一件事情需要注意,全班每个同学愿意帮忙的好感度有高有低(注意:小渊和小轩的好心程度没有定义,输入时用0表示),可以用一个0-100的自然数来表示,数越大表示越好心。
小渊和小轩希望尽可能找好心程度高的同学来帮忙传纸条,即找到来回两条传递路径,使得这两条路径上同学的好心程度之和最大。
现在,请你帮助小渊和小轩找到这样的两条路径。
输入格式
第一行有2个用空格隔开的整数 mm 和 nn,表示学生矩阵有 mm 行 nn 列。
接下来的 mm 行是一个 m∗nm∗n 的矩阵,矩阵中第 ii 行 jj 列的整数表示坐在第 ii 行 jj 列的学生的好心程度,每行的 nn 个整数之间用空格隔开。
输出格式
输出一个整数,表示来回两条路上参与传递纸条的学生的好心程度之和的最大值。
数据范围
1≤n,m≤501≤n,m≤50
输入样例:
3 3
0 3 9
2 8 5
5 7 0
输出样例:
34
public static void main(String[] args) {
int n = in.nextInt();
int m = in.nextInt();
int[][] arr = new int[n + 1][m + 1];
for (int i = 1; i < n + 1; i++)
for (int j = 1; j < m + 1; j++) {
arr[i][j] = in.nextInt();
}
int[][][] dp = new int[n + m + 1][n + 1][n + 1];
for (int k = 2; k < n + m + 1; k++) {
for (int i = 1; i < n + 1; i++) {
for (int i2 = 1; i2 < n + 1; i2++) {
int j = k - i;
int j2 = k - i2;
if (j >= 1 && j <= m && j2 >= 1 && j2 <= m) {
int add = arr[i][j];
if (i != i2) add += arr[i2][j2];
dp[k][i][i2] = Math.max(dp[k][i][i2], dp[k - 1][i - 1][i2 - 1] + add);
dp[k][i][i2] = Math.max(dp[k][i][i2], dp[k - 1][i][i2 - 1] + add);
dp[k][i][i2] = Math.max(dp[k][i][i2], dp[k - 1][i - 1][i2] + add);
dp[k][i][i2] = Math.max(dp[k][i][i2], dp[k - 1][i][i2] + add);
}
}
}
}
out.println(dp[n + m][n][n]);
out.flush();
out.close();
}
